写在前面
将世界终结前最后的画面,
配上的将会是怎样的旁白。
——《世末积雨云》
开始了
后缀自动机,就是 $1$ 个可以识别字符串的所有子串的有限状态自动机。
我们要学的是最简状态后缀自动机。不是最简的就不如暴力了。
然后我们可以对子串问题说 bye bye 啦。(雾
有限状态自动机
终于理解了这玩意。
性(gan)感(xing)理解。
就是字符串集(状态)的转移。
从 $init$(空集) $1$ 步步到转移到 $end$(最终状态) 的各种过程。
举个例子,在 $kmp$ 中,字符串:$aabaab$ 中 状态 $aabaa$ 可以 (-‘$b$’->) 转移到 $aabaab$,也可以 (-$fail$->) 转移到 $aa$
总结 1 下,
$alpha$:字符集
$init$:初始状态
$end$:结束状态
$state$:状态
$trans(state,ch)$:状态 $state$ 通过 $ch$ 手段转移到的状态,可以理解为 $1$ 条连边,边权是转移方式。
用上例来讲,$aa=trans(aabaa,fail)$
开始的说明
$alpha$:当然是 [‘$a$’,’$z$’] 啦
$init$:当然是空串(‘‘)啊
$end$:是 $1$ 个后缀
$state$:下面会讲
$trans$:就是很朴素的加字符串转移(-$char$->),没有什么失配 $fail$。
朴素
考虑很沙雕的做法。
把每个后缀扔进 $trie$ 树,这样我们就有了状态数为 $n^2$ 的后缀自动机啦。
状态的表示及压缩
状态的压缩:reg 集合
我们先定义 $1$ 个叫 $reg$ 集合的东西
$reg(s)$ 表示从状态 $s$ 开始,能转移到的所有的状态 $s’$ 的集合,包括 $s$ 自己。
比如在 $abac$ 中 状态”$a$” 的 $reg$ 为:”$a$”,”$ab$”,”$aba$”,”$abac$”,”$ac$”
所以很显然的我们能想到 $reg$ 集相同的状态,可以合并,因为其对后的转移是 $1$ 模 $1$ 样的。
注意这时,我们的状态不再是 $1$ 种字符串,而是字符串集了。
状态的表示:right 集合
我们用 $1$ 种更形象简易的方法表示 $reg$
因为 $trans$ 的形式我们观察 $1$ 下,只是 $+ch$
比如 $abac$ 中的第 $1$ 个 “$a$”,可以转移到:”$a$”,”$ab$”,”$aba$”,”$abac$”,也就是后缀”$abac$”的每 $1$ 个前缀。
所以我们只用记住 $1$ 个后缀,也就是 $1$ 个位置,就可以得到 $1$ 系列转移。
状态 “$a$”,我们可以表示为:${1,3}$,而 ${1,3}$ 却不 $1$ 定能代表 “$a$”
再来 $1$ 个例子 “$abab$” 对于状态 ${2,4}$ 可以表示 “$b$” 和 “$ab$”,因为它们对后的转移是 $1$ 样的。
而 ${2,4}$ 是字符串的右端点,所以此集合就叫做 $right$ 集合。
仅需要记住 $1$ 些右端点,就可以简易的表示 $1$ 个状态。
总结 $1$ 下,$right$ 集合是简易表示状态的方法,是等价于 $reg$ 的。
这是,我们就可以随便用 $right$ 集表示状态,在后面的部分,我可能弄混,不过不管了。
right 集合的性质
right 集合所表示的字符串集
原串叫做:$st$
我们先假定 $1$ 个长度 $len$,我们有 $1$ 个 $right$ 集合 ${r_i}$
如果子串 $st[r_i-len,ri)$ 都相等。那字符串 $st[r_i-len,r_i)$ 就能被该 $right$ 集表示。
而当 $len$ 过小,$ | right | $ 就会增大
而当 $len$ 过大,$ | right | $ 就会缩小
所以我们可以知道,$1$ 个 $right$ 所能表示的字符串,就是 $st[r_i-[min,max],r_i)$
我们可以对 $right$ 再记住 $1$ 个区间 $[min,max]$ 就可以知道 $right$ 集合所表示的字符串集
right 集合间的关系
$right$ 集合之间有联系吗?
有也,巨大!
我们先拿来 $2$ 个 $right$ 集合 $A$,$B$
如果,$2$ 个集合不交,那就不交喽。
如果,$2$ 个集合相交,结论先立在这,那必定有包含关系。
我们令交点为 $r$,$A$ 集的 $right$ 集叫 $right_A$,$[min,max]$ 叫 $[min_A,max_A]$。$B$ 也 $1$ 样。
我们令 $max_A < min_B$ 那么就有 $st[r-max_A,r)$ 是 $st[r-min_B,r)$ 的后缀。
因此对于 $right_B$ 中的每 $1$ 个 $st[r_i-min_B,r_i)$,$st[r_i-max_A,r_i)$ 也会出现。
而 $len$ 小,$ | right | $ 大,所以 $right_B∈rightA$
总结 $1$ 下 $right$ 集合之间,要么不相交,要么互相包含。
parent 树
parent 树的定义
根据 $right$ 集合的从属关系,我们就可以构建与 $right$ 有关的 $parent$ 树
若 $2$ 个 $right$ 集合 $A$,$B$,$B$ 是包含 $A$ 的所有集合中的大小最小的集合。
$B$ 就是 $A$ 的父亲。
这样 right 集合就会形成 1 个树形结构。
线性状态的证明
引用 WJMZBMR 的图:
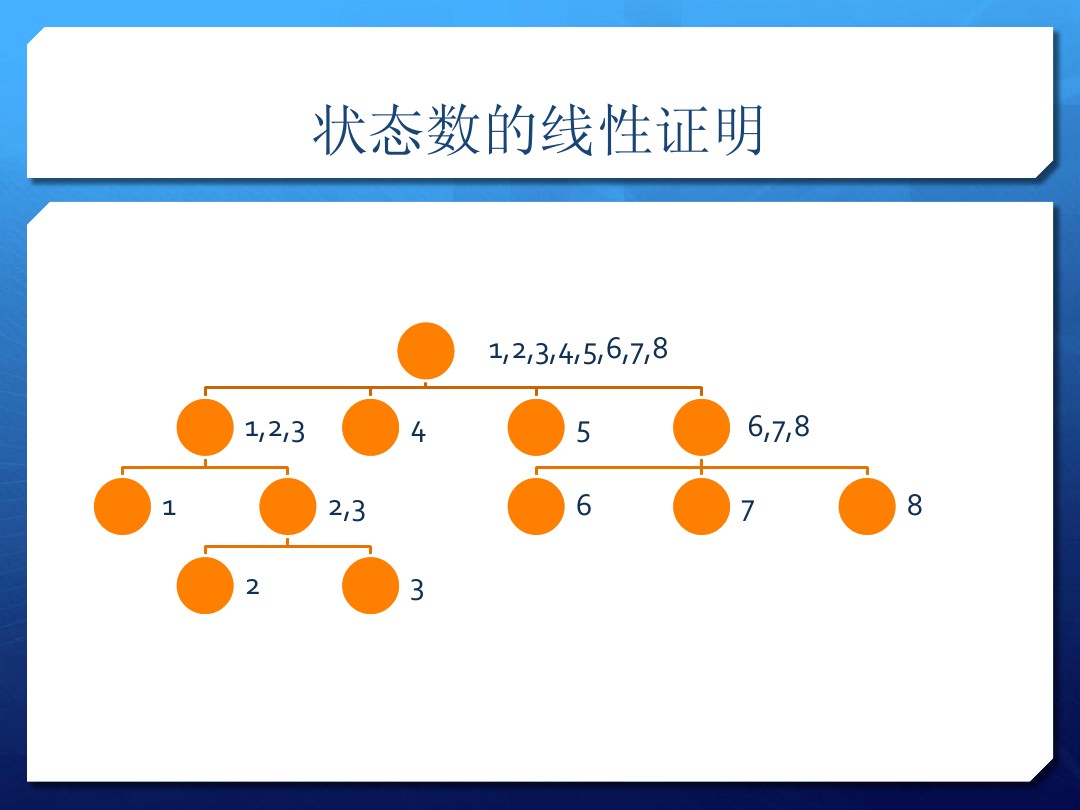
我们可以显然(?)的发现,状态数是 $O(n)$ 的,最多 $2n$。
想想线段树?
用 parent 树记录 right 集
我们不可能对每一个状态的 $right$ 集合都记录,但我们通过 $parent$ 树,得到的 $right$ 集的包含关系后,我们可以发现:
状态 $u$ 的 $right$ 集是以 $u$ 为根的子树的 $right$ 集的并集。
而集合归根到底元素有关,所以我们只要知道每个元素最开始在哪里出现(构造的时候会讲在哪),之后的并上去就好了。
不会有 $2$ 个元素同时在 $1$ 个结点最先出现。
| 因为如果有集合 ${ri_a,ti_b | ri_a < ri_b}$ 出现,那么必有集合 ${ri_b}$ |
${ri_b}$ 能表示的 $len$ 肯定能更长。
转移的线性证明
不会啊,感性理解,感性理解,不会对理解有影响的,略了。
再谈 len 区间
和 parent
$min_A=max_{fa_A}+1$
还是那句话 $len$ 小,$ | right | $ 大。
所以我们没有必要记住 $min$
和 trans
我们考虑转移时,从状态 $A$,$+ch$ 转移到状态 $B$,也就是多加了 $1$ 个字符。
| 若 $right_A$ 是 ${r_i}$,那 $rigth_B$ 就是 ${r_i+1 | st[r_i+1]=ch}$ |
我们可以得到 $max_B>max_A$
这个性质很重要。
抱歉
终于讲完前置知识了。
好肝啊!!!!!!!!!!
不过理解了这些,做题就很容易啦。
后缀自动机的线型构造法
写在前面
此过程是在线的。
考虑假如 $1$ 个字符 $ch$,对原来状态的影响。
而对于每 1 个状态,我们需要明确我们需要干什么,求出它的什么信息。
1,$trans$ 它的转移。
2,$parent$ 在 $parent$ 树上的父亲。
3,$len$ 即 $maxlen$,因为只用记 $1$ 个,就用 $len$ 吧。
1 堆定义
原来字符串的长度为 $L$,加入后会变成 $L+1$。
对于上 $1$ 次的 $L$,$1$ 定会有 $1$ 个状态($right$ 集)是 ${L}$,也就代表整个字符串,记为 $last$。
找到状态
我们考虑转移,其实也就是 $right$ 集合中包含元素 $L$ 的才会转移,我们可以通过 $parent$ 树很方便的找到这些状态。
也就是,$parent$ 树上 $last$->$root$ 的路径上的状态。
我们把这些状态记作:$u_1=last,u_2=fa_{last},\dots,u_n=root$
开始转移
我们先新建 $1$ 个状态,叫 $newlast$,它的转移没有,父亲暂定,$len_newlaast=len_last+1$,它代表的是 $right$ 集合是 ${L+1}$
| 我们尝试着把每个 $right$ 集 ${r_i}$ 都变成 ${r_i+1 | st[r_i+1]=ch}$ |
也就是对于每 $1$ 个状态,加 $1$ 个 $+ch$ 的转移($trans$)
而我们发现,会有 $1$ 个 $u_p$,已经有 $+ch$ 的转移了。
并且由于 $right$ 集的包含关系,那么 $u_p,\dots,u_n$ 也有 $+ch$ 的转移。
那么我们就让 $p$ 的第 $1$ 个有 $+ch$ 的转移的状态。
然后我们先把 $u_1,\dots,u_{p-1}$ $+ch$ 转移到 $newlast$
这样我们就搞定了 $u_1,\dots,u_{p-1}$ 的更新。
这时,对于 $u_p,\dots,u_n$ 我们可以分类讨论:
A:不存在 $p$,那么就很好办,让 $fa_{newlast}=root$ 就好。
B:存在,我们可以再进行讨论。
我们先令 $q=trans(p,->ch)$
Ba:当 $len_p+1=len_q$ 我们可以直接 $fa_{newlast}=q$ 转移就好,这也相当于给 $q$ 上路径加了元素 $L+1$。
Bb:当 $len_p+1 < len_q$ 我们就不能直接转移。
举个例子:
$st=aaaxaaaxaa+x$
$L=10$
$right_p={3,7,10}$ $len_p=2$
$right_q={4,8}$ $len_p=4$
而直接转移的话,$right_{q’}={4,8,11}$ 但 $len_{q’}=3≠4$,会出问题。
不过也很好(??)解决,直接新建 $1$ 个克隆点,叫做 $nq$ 令它的 就好了。
如何克隆?
1,$len_{nq}=len_p+1$
2,$fa_{nq}=fa_q$ $fa_q=nq$
3,把 $q$ 的 转移($trans$)复制到 $nq$
4,$u_p,\dots,u_n$ 中 $trans(u_i,->ch)=q$ 的转移改成 $nq$。
如何转移?
$fa_{np}=nq$
总结 1 下
1,新建 $newlast$
2,找到 $p$
3,解决 $u_1,\dots,u_{p-1}$ 的转移
4,解决 $u_p,\dots,u_n$ 的转移
分类讨论:
4,A
4,Ba
4,Bb
5,更新 $last$
代码!
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int ML=1000100;
const int ML2=ML<<1;
const int C=26;
struct Asam //Aspe's sam
{
int tpsam,rt,la; //root,last
int fa[ML2],len[ML2],tr[ML2][26]; //父亲,maxlen,
int neW(int llen) //新建状态
{
int np=tpsam++;
fa[np]=-1; len[np]=llen;
for (int i=0; i<C; i++) tr[np][i]=-1;
return np;
}
void iniT() { tpsam=0; rt=la=neW(0); } //初始化,建立 root(起始状态)
void inS(int ch)
{
int np=neW(len[la]+1),p; //新建
for (p=la; ~p && !~tr[p][ch]; p=fa[p]) tr[p][ch]=np; //找 p 且转移
if (~p) //类型 B
{
int q=v[p][ch];
if (len[p]+1==len[q]) fa[np]=q; //类型 Bb
else //类型 Ba
{
int nq=neW(len[p]+1);
fa[nq]=fa[q]; fa[q]=fa[np]=nq;
for (int i=0; i<C; i++) tr[nq][i]=tr[q][i];
for ( ; ~p && tr[p][ch]==q; p=fa[p]) tr[p][ch]=nq;
}
}
else fa[np]=rt; //类型 A
la=np; //更新 last
}
}sam;
char st[ML];
int main()
{
scanf("%s",st);
sam.iniT();
for (int i=0,len=strlen(st); i<len; i++) sam.inS(st[i]-'a');
return 0;
}
应用
子串个数?
假如子串在状态 $S$ 中。
| 那么个数就是 $ | right_S | $ |
我们只要求 $1$ 个 $right$ 集的大小就好(太容易啦
只要在 $parent$ 树的子树中统计 $1$ 下元素的个数
考虑每 $1$ 次新建结点,就会有 $1$ 个新元素出现,标 $1$ 个 $1$,到时算 $1$ 子树大小就好。
| 考虑 $1$ 中比较容易的实现方法,就是 $len$ 越大的 $ | right | $ 越小,所以我们把 $len$ 排序后,倒序就是 $1$ 种拓扑序啦。 |
luogu 模板:求 $max(len_{substring} * times_{substring})$ 注意次数要大于 1
算出次数就好。
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int ML=1000100;
const int ML2=ML<<1;
struct Asam
{
int tpsam,rt,la;
int fa[ML2],si[ML2],len[ML2],v[ML2][26];
int neW(int llen,int ssi)
{
int np=tpsam++;
fa[np]=-1; len[np]=llen; si[np]=ssi;
for (int i=0; i<26; i++) v[np][i]=-1;
return np;
}
void iniT() { tpsam=0; rt=la=neW(0,0); }
void inS(int ch)
{
int np=neW(len[la]+1,1),p;
for (p=la; ~p && !(~v[p][ch]); p=fa[p]) v[p][ch]=np;
if (~p)
{
int q=v[p][ch];
if (len[p]+1==len[q]) fa[np]=q;
else
{
int nq=neW(len[p]+1,0);
fa[nq]=fa[q]; fa[q]=fa[np]=nq;
for (int i=0; i<26; i++) v[nq][i]=v[q][i];
for ( ; ~p && v[p][ch]==q; p=fa[p]) v[p][ch]=nq;
}
}
else fa[np]=rt;
la=np;
}
int c[ML2],p[ML2];
void counT_sizE()
{
for (int i=0; i<tpsam; i++) c[len[i]]++;
for (int i=1; i<tpsam; i++) c[i]+=c[i-1];
for (int i=tpsam-1; ~i; i--) p[--c[len[i]]]=i;
for (int i=tpsam-1; i; i--) si[fa[p[i]]]+=si[p[i]];
}
long long calc()
{
counT_sizE();
long long ans=0;
for (int i=1; i<tpsam; i++)
if (si[i]>1) ans=max(ans,1LL*si[i]*len[i]);
return ans;
}
}sam;
char st[ML];
int main()
{
scanf("%s",st);
sam.iniT();
for (int i=0,len=strlen(st); i<len; i++) sam.inS(st[i]-'a');
cout<<sam.calc();
return 0;
}
知道次数我们就可以玩很多东西了。
总总结
SAM 码熟后真的容易打。
只要熟知性质即可。
进阶:NOI2018 你的名字 题解:NOI2018 你的名字
CC 原创文章采用CC BY-NC-SA 4.0协议进行许可,转载请注明:“转载自:后缀自动机的实现及应用”