数据结构 胜者树

胜者树的简单实现

用来写 dijkstra

Posted by Aspe on September 23, 2018

何为胜者树？

先会线段树再会胜者树的都是越俎代庖。
不知道胜者树的而会线段树的都是大佬。
胜者树是线段树的前置知识。

胜者树用于维护固定区间的最大值，且只支持单点修改，完全可以用线段树代替。
也可以这样理解，1 个静态的堆。
但是进日貌似发现这个有个好实现的写法，并且希望大家不要忘了有这个东西，所以写了此 blog

并且用胜者树去做 1 些问题会比较贴切，因为堆中许多会有重复。
用它优化 dijkstra 是坠吼的。

胜者树

胜者树

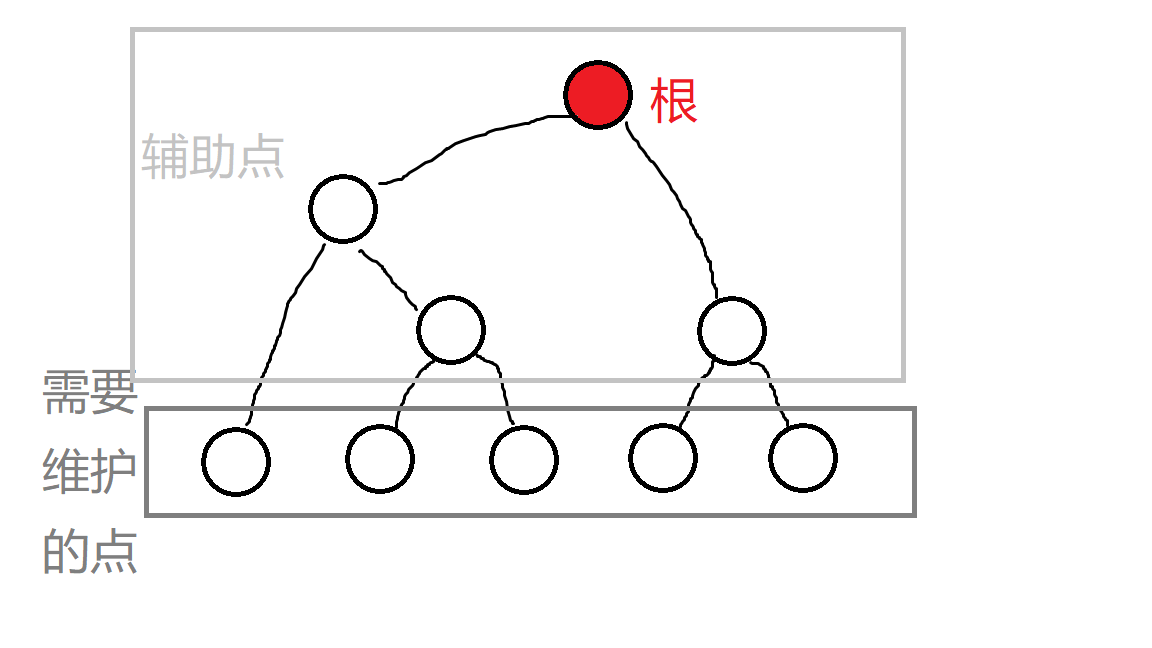
单点改动后，顺着父亲维护，根就维护整个区间的信息了。
所谓胜者树，就是两两比较，决出胜者，更进 1 层。就像决出冠军 1 样，形象的数据结构。
这个东西会很好实现吗？是的！！！

约定

假设区间大小为 n，是 [0,n)。

建树 && 映射

其实 1 个数组 win[] 就可以表示这棵树了，所表示的是：树上该结点的优胜者，在区间中的位置。
辅助点为 [1,n)
维护点为 [n,2n)

区间中第 k 个位置，在胜者树的哪里呢，也就是直接 k+n 就好了

这样 1 个简单的规定，却会有 1 个非常的性质。

设 p 是树上结点，那么：

p/2 是 p 的父亲
p2 是 p 的左儿子
p2+1 是 p 的右儿子

建树 2 行：

//build
for (int i=0; i<n; i++) win[i+n]=i+1; //维护点的初始化
for (int i=n-1; i; i--) win[i]=choose_winner(win[i*2],win[i*2+1]); //辅助点的初始化

维护

假设区间中第 k 个元素要变动，然后更新整棵树怎么办

//updata
for (int p=k/2; p; p>>=1) win[p]=choose_winner(win[p*2],win[p*2+1]); //choose_winner 时具体情况而定

查询

没什么好说的了

win[1] 就是改区间的优胜者

模版

以单源最短路为例。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>

using namespace std;

const int MLm=200100;
const int MLn=100100;
const int oo=1023333333;

struct Tedge { int v,w,nx; }lb[MLm];

int toP[MLn],tplb;

void CSH() { memset(toP,-1,sizeof toP); tplb=0; }

void inS(int u,int v,int w)
{
	int np=tplb++;
	
	lb[np].v=v; lb[np].w=w; lb[np].nx=toP[u];
	
	toP[u]=np;
}

int d[MLn],dis[MLn],wiN[MLn*2],n;

void updatA(int p,int x) //有 -1 麻烦 1 点
{
	d[p]=x;
	
	for (p=(p-1+n)/2; p; p>>=1)
	{
		int lc=p*2,rc=p*2+1;
		
		if (d[wiN[lc]]==-1) { wiN[p]=wiN[rc]; continue; }
		if (d[wiN[rc]]==-1) { wiN[p]=wiN[lc]; continue; }
		
		if (d[wiN[lc]]<d[wiN[rc]]) wiN[p]=wiN[lc];
		                      else wiN[p]=wiN[rc];
	}
}

void dijkstrA(int s)
{
	for (int i=1; i<=n; i++) d[i]=oo;
	//初始化
	for (int i=0; i<n; i++) wiN[i+n]=i+1;
	for (int i=n-1; i; i--) wiN[i]=wiN[i*2];
	
	updatA(s,0);
	
	for ( ; ; )
	{
		int u=wiN[1];
		
		if (d[u]==-1 || d[u]==oo) break;
		
		dis[u]=d[u];
		
		for (int kb=toP[u]; ~kb; kb=lb[kb].nx)
		{
			int v=lb[kb].v,w=lb[kb].w;
			
			if (d[u]+w<d[v]) updatA(v,d[u]+w);
		}
		
		updatA(u,-1);
	}
}

int main()
{
	int m,s; scanf("%d%d%d",&n,&m,&s);
	
	CSH();
	
	for (int i=0; i<m; i++)
	{
		int u,v,w; scanf("%d%d%d",&u,&v,&w);
		
		inS(u,v,w);
	}
	
	dijkstrA(s);
	
	for (int i=1; i<=n; i++) printf("%d ",dis[i]);
	
	return 0;
}
CC 原创文章采用CC BY-NC-SA 4.0协议进行许可，转载请注明：“转载自：胜者树的简单实现”
CATALOG
    FRIENDS