树上 01背包
例题:最佳团体
又是 1 种时间复杂度看起来立方,实则均摊是平方的方法。
在树上选 k 个点,使点权和最大,选每个点必须要选他的父亲。
f[u][k]=f[son][k’] 的 01背包
我们设 f[u] 是前 i 个孩子合并后的背包,现在要把第 i+1 个孩子 f[v] 合并进去
设背包推到的最大容量是 size
那么我们这 1 步的耗时(操作步数)要做到成这样:f[u].size*f[v].size
for (int j=si; j>=0; j--)
for (int i=0; i<=vsi; i++)
f[u][j+i]=max(f[u][j+i],f[u][j]+f[v][i]);
si+=vsi;
写成这样,复杂度均摊就是平方级别的了。
虚树
其实并不是什么高大上的东西。
当我们需要做多次小型的 树型DP 时,发现有些点是无关紧要的,好像只和某些 lca 有关。
对于每次小型 树型DP ,询问的点数是 ki,那我们就用它们和它们的做 DP 所需要的 lca 构成的规模为 2ki 的小树,就是虚树。
虚树,只是把 DP 的规模缩小。
来看经典例题:消耗战
题意就不详细的说,大概是,每次询问树上 1 些点的最小割。
当我们先不考虑虚树构建,假设虚树已经构造好了,
我们用 f[u] 表示切割子树 u 所花费的最小代价,
那么 f[u]=sum(min(edge[u->v],f[v]))
v 是 u 在虚树中的孩子,edge 是 2 点间的最短边权,其实这里只用求点到根结点的最短边权。
现在我们就可以知道,我们需要构造的虚树的性质了。
就像这样子:
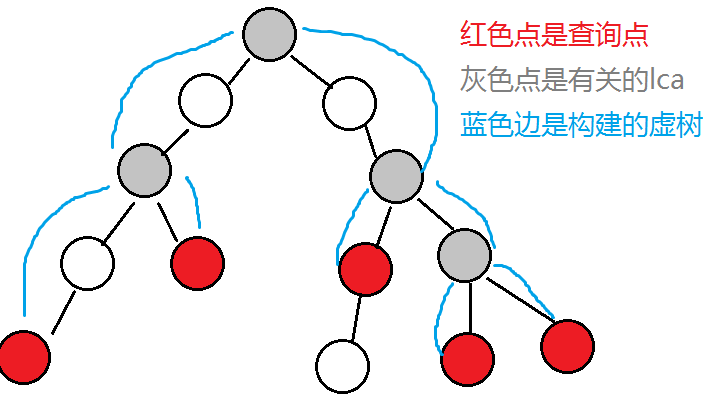
我们“感性”的发现,好像是把询问点从“左”往“右”两两之间做 lca,就是那些有关的 lca 了。
可是怎么从左往右?
在“感性”的想,其实就是按 dfs序 排序,之前我有提到,dfs序 其实是个很强大的东西,它现在对构建虚树起到关键性作用。
所以我们把询问点按 dfs序 排序,两两求 lca 就得到构建虚树的所有点了。重复的点后面会提。
现在是如何连边?
我们再大力的把点按 dfs序 再排 1 次序,因为 dfs序 有个很好的性质:父结点肯定在子结点前面
所以,我们找每个 结点v 的 父结点u,也就是满足 v 在 u 的子树中且 u 的 dfs 序最小,
我们可以得到做法:
for (int i=1,np=p[0]; i<k; i++) //np 是 p[i] 可能的父结点,fa[u] 是 u 的父结点
{
for ( ; loW[np]>loW[p[i]] || hiG[np]<loW[p[i]]; np=fa[np]); //若 p[i] 不在 np 的子树里,np 就往上跳到 fa[np]
if (np!=p[i]) inS(np,p[i],mi[p[i]]),fa[p[i]]=np,np=p[i]; //找到 p[i] 的父亲,np 向下逼近
}
若把 np 理解成栈,1 但出去了,就进不来,所以时间复杂度是没问题的。
总结,我的虚树构建法,就是先找点,再连边,附上核心代码:
int k; scanf("%d",&k);
for (int i=0; i<k; i++) scanf("%d",&p[i]),f[p[i]]=q;
sort(p+0,p+k,cmP);
for (int i=1,kk=k; i<kk; i++) p[k++]=lcA(p[i-1],p[i]);
sort(p+0,p+k,cmP);
for (int i=0; i<k; i++) toP[p[i]]=-1; tplb=0;
for (int i=1,np=p[0]; i<k; i++)
{
for ( ; loW[np]>loW[p[i]] || hiG[np]<loW[p[i]]; np=nx[np]);
if (np!=p[i]) inS(np,p[i],mi[p[i]]),nx[p[i]]=np,np=p[i];
}
CC 原创文章采用CC BY-NC-SA 4.0协议进行许可,转载请注明:“转载自:树型DP”