定义：
一如既往的来下个定义：
1，并不是可以帮我们自动AC的东东。
2，不用理解自动机的定义也没关系（其实是我看不懂啦）
所以，AC自动机是个什么算法呢？是一种多匹配算法。
相比于KMP的一个串匹配另一个串，AC自动机是一个串匹配一个字典。
举个例子，就好比在网站注册用户名时，系统会检测是否与其他人重名，AC自动机是用于解决类似的问题的算法。
也就是说，AC自动机是一个解决一堆模式串，与一个文本串匹配问题的算法。
例题：
洛谷裸题
给定n个模式串和1个文本串，求有多少个模式串在文本串里出现过。
模式串：a;aa;aaa
文本串：aaaa
输出：3
模式串总长10^6，文本串同。
引入
正文开始！
首先我们要明白，AC自动机其实就是解决字典问题的Trie与解决匹配问题的KMP结合起来的。
下文在分析Trie与KMP的逻辑关系时，就是AC自动机的实现了。
Trie暴力
首先第一步，把模式串建立Trie树。设文本串为S
试图只用Trie解决问题，枚举S的出发位置p，也就是枚举S的后缀，把每个后缀在Trie上找一遍，就可以了。
请大家务必仔细理解Trie树，字符串是被记录在Trie树上’根结点’到一个结点的路径上，结点上还记录着该字符串出现的次数（可以为0）。
这时，便用KMP的思想优化，也就是失配时的跳跃操作。
后缀结点与Trie图
引入概念：1，后缀结点。2，Trie图。
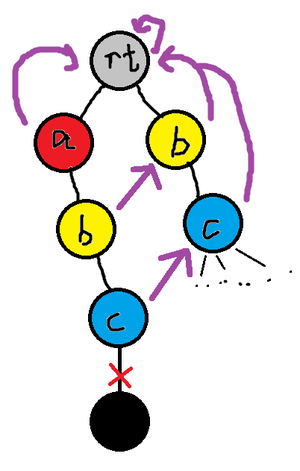1，左b指向右b，右b所在的结点是左b所在的结点的后缀结点
2，左b向右b连一条边，即每个节点与其后缀节点连一条边，在Trie树的基础上，构成Trie图。
可以发现，在S{…abc$….}与模式串“abc*….”匹配不成功时，可以跳到c的后缀结点上即与模式串“bc….”匹配。如果再不成功，就继续跳
所以后缀结点的定义就是：记另一点为k，s1是root->p代表的字符串，s2是root->k的代表字符串。s2是s1的后缀且s2最长（其他情况将被包含在s2中）。则k就是p的后缀结点。s1,s2均为Trie上的串。
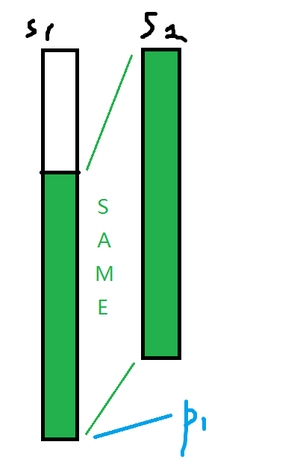
如可求后缀结点？如何查询？注意事项
如何求后缀结点？如何查询？注意事项？
先讲查询，跟KMP的套路一样。
把文本串顺着Trie找，找不到就等价的跳到后缀节点上，直到找到或到达根结点。
算某个点k的后缀节点其实也跟查询k所对应的字符串差不多 ，先构造BFS序，然后递推。
根节点和第二层节点的后缀节点就是根节点（这是边界）（类似于KMP）；
对于其他某个节点K，我们可以临时定义S为K的父节点的后缀节点，c为到达K的边的字符，然后如果S没有c边，就一直取S为它的后缀节点，直到S为根节点或S有c边。
若想理解上面这句话，必须认真理解后缀结点的概念。并可以结合图。
注意，在查找的时候，在Trie上找到了相等的串，也就代表它的子串也是一样的，这相当于该串的后缀结点形成的路径上的串都找到了。还需注意的是，每个点是只算一次，还是多次。这是一个“后缀连接”的问题，详细见：大佬的博客。
时空复杂度
时空复杂度？
空间：一个Trie，O(30n)左右，比较大。
时间：跟KMP的证明一样，跳跃时，虽然减去的数比较难统计，但加却每次只加1，所以是O(n)的。
或，查询时，相当于每次跳跃，初始结点p就往后移，所以最多移n次。
总结
总结，AC自动机，就是Trie上用KMP优化，是两种算法的有机结合，是非常强大的字符串处理算法。 两种不同算法，相互结合，便有了巨大的力量。
模版
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int ML=1000100;
struct Ttrie { int son[26],con,nx; }ac[ML];
int tpzd;
int New()
{
int np=tpzd++;
Ttrie &t=ac[np];
memset(t.son,-1,sizeof t.son); t.con=0;
return np;
}
void Ins(int np,char *st,int k,int n)
{
if (k==n) { ac[np].con++; return; }
int &so=ac[np].son[st[k]-'a'];
if (so==-1) so=New();
Ins(so,st,k+1,n);
}
int op[ML],de[ML]; //op:队列 de:deep
void Bfs(int rt)
{
op[0]=rt; de[rt]=1; ac[rt].nx=rt;
for (int Head=0,Tail=1; Head<Tail; Head++)
{
int u=op[Head];
for (int kb=0; kb<26; kb++)
{
int v=ac[u].son[kb];
if (v==-1 || de[v]) continue;
de[v]=de[u]+1; op[Tail++]=v; //获得BFS序
if (de[v]<3) ac[v].nx=rt;
else
{
int &p=ac[v].nx;
for (p=ac[u].nx; ; p=ac[p].nx)
{
if (ac[p].son[kb]!=-1)
{
p=ac[p].son[kb];
break;
}
if (p==rt) break;
}
}
//跟上面讲的方法一样
//提醒：
//进入递归的是父亲结点的后缀结点
//要先检验有没有可行的边再检验是不是根
}
}
}
void Print(int np) //调试
{
if (np==-1) return;
Ttrie t=ac[np];
for (int i=0; i<26; i++) cout<<t.son[i]<<" ";cout<<endl;
cout<<t.con<<" "<<t.nx<<endl;
for (int i=0; i<26; i++) Print(t.son[i]);
}
int Find(char *st,int len,int rt)
{
int ans=0;
for (int i=0,p=rt; i<len; i++)
{
int ch=st[i]-'a';
for ( ; ; ) //跳跃
{
if (p==rt) break;
int np=ac[p].son[ch];
if (np!=-1) break;
p=ac[p].nx;
}
if (ac[p].son[ch]!=-1) //查找成功
{
p=ac[p].son[ch];
for (int np=p; np!=rt && ac[np].con!=-1; )
{
ans+=ac[np].con; ac[np].con=-1; //去重
np=ac[np].nx;
}
//路径处理
}
}
return ans;
}
char s[ML];
int main()
{
int n; scanf("%d",&n);
int rt=New(); //根节点建立
for ( ; n; n--)
{
scanf("%s",s);
Ins(rt,s,0,strlen(s)); //构建Trie
}
Bfs(rt); //求后缀结点
scanf("%s",s);
int len=strlen(s);
cout<<Find(s,len,rt); //查询
return 0;
}
/*
3
c
bc
abc
*/
CC 原创文章采用CC BY-NC-SA 4.0协议进行许可，转载请注明：“转载自：AC自动机”